bLSAG ring signatures overview

2022-07-20

Note: I’m not a mathematician, I’m just an amateur on math. These notes are just an attempt to try to sort the notes that I took while learning abut bLSAG.

bLSAG: Back’s Linkable Spontaneous Anonymous Group signatures

signer ambiguity
linkability
unforgeability

Setup

Let $G$ be the generator of an EC group. We use a hash function $\mathcal{H}_p$, which maps to curve points in EC, and a normal hash $\mathcal{H}_n$, which maps to $\mathbb{Z}_p$. Signer’s key pair: $k_{\pi}$, s.t. $K_{\pi} = k_{\pi} \cdot G \in \mathcal{R}$, with secret index $\pi$. Set of Public Keys: $\mathcal{R} = \{ K_1, K_2, \ldots, K_n \}$

def new_key():
    k = F.random_element()
    K = g * k # g is the generator of the EC group
    return K

Signature

compute key image: $\tilde{K} = k_{\pi} \mathcal{H_p} ( K_{\pi}) \in G$
```
key_image = k * hashToPoint(K)
```
Generate $\alpha \in^R \mathbb{Z}_p$, and $r_i \in^R \mathbb{Z}_p$, for $i \in \{1, 2, \ldots, n \}$, with $i \neq \pi$
- $r_i$ is used for the fake responses
```
a = F.random_element()
r = [None] * len(R)
for i in range(0, len(R)):
    if i==pi:
        continue


    r[i] = mod(F.random_element(), p)
```
Compute $c_{\pi + 1} = \mathcal{H}_n ( m, [\alpha G], [\alpha \mathcal{H}_p(K_{\pi})])$
```
c[pi1] = hash(R, m, a * g, hashToPoint(R[pi]) * a, p)
```
for $i=\pi + 1, \pi +2, \ldots, n, 1, 2, \ldots, \pi -1$, calculate, replacing $n+1 \rightarrow 1$ $$ c_{i+1} = \mathcal{H}_n (m, [r_i G + c_i K_i], [r_i \mathcal{H}_p (K_i) + c_i \tilde{K}]) $$
- Notice that (from step 3 & 4):
  $\alpha \mathcal{H}_p (K_{\pi}) = r_{\pi} \mathcal{H}_p (K_{\pi}) + c_{\pi} \cdot (\tilde{K})$,
  where $\tilde{K}= k_{\pi} \mathcal{H_p} ( K_{\pi})$, so:
  $\alpha \mathcal{H}_p (K_{\pi}) = r_{\pi} \mathcal{H}_p (K_{\pi}) + c_{\pi} \cdot (k_{\pi} \mathcal{H}_p(K_{\pi}))$
  which is equal to,
  $\alpha \cdot \mathcal{H}_p (K_{\pi}) = (r_{\pi} + c_{\pi} \cdot k_{\pi}) \cdot \mathcal{H}_p(K_{\pi})$
  From where we can see: $\alpha = r_{\pi} + c_{\pi} \cdot k_{\pi}$
  which we can rearrange to $r_{\pi} = \alpha - c_{\pi} \cdot k_{\pi}$.
```
for j in range(0, len(R)-1):
    i = mod(pi1+j, len(R))
    i1 = mod(pi1+j +1, len(R))


    c[i1] = hash(R, m, r[i] * g + c[i] * R[i],
            r[i] * hashToPoint(R[i]) + c[i] * key_image, p)
```
Define $r_{\pi} = \alpha - c_{\pi} k_{\pi} \mod{p}$

r[pi] = mod(a - c[pi] * k, p)

Signature: $\sigma(m) = (c_1, r_1, \ldots, r_n)$, with key image $\tilde{K}$ and ring $\mathcal{R}$. - $len(\sigma(m)) = 1+n$

return [c[0], r]

Step by step (simplified):

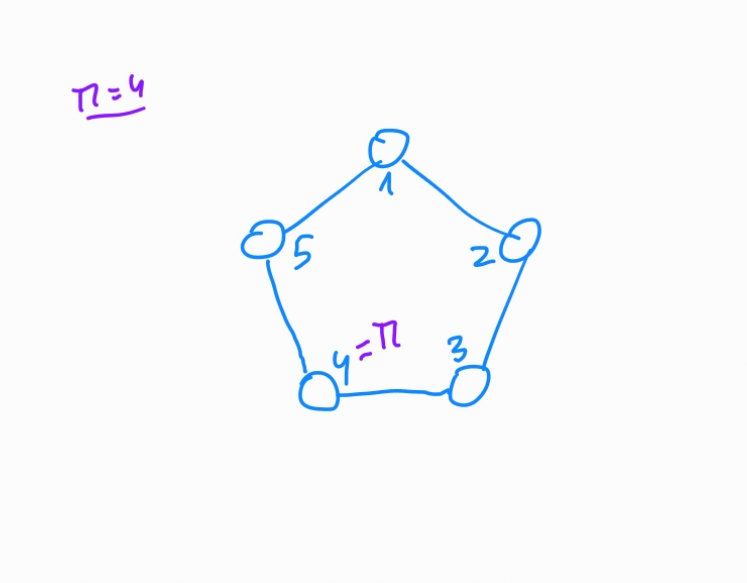
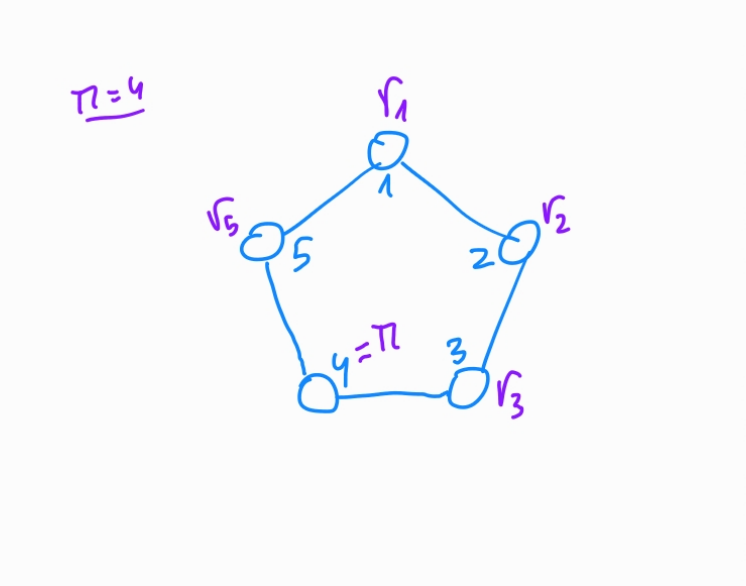
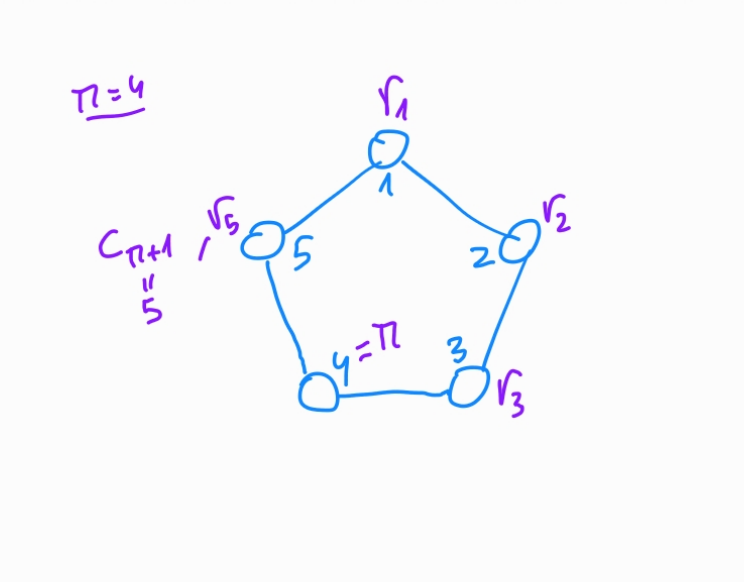
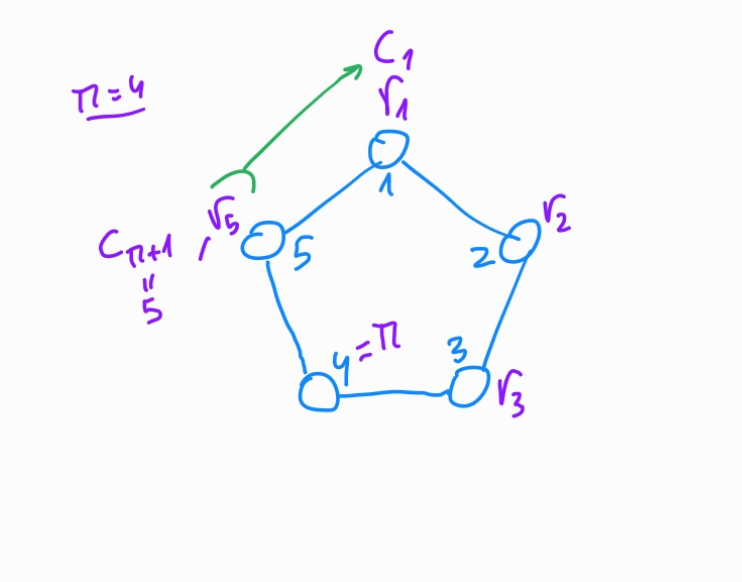
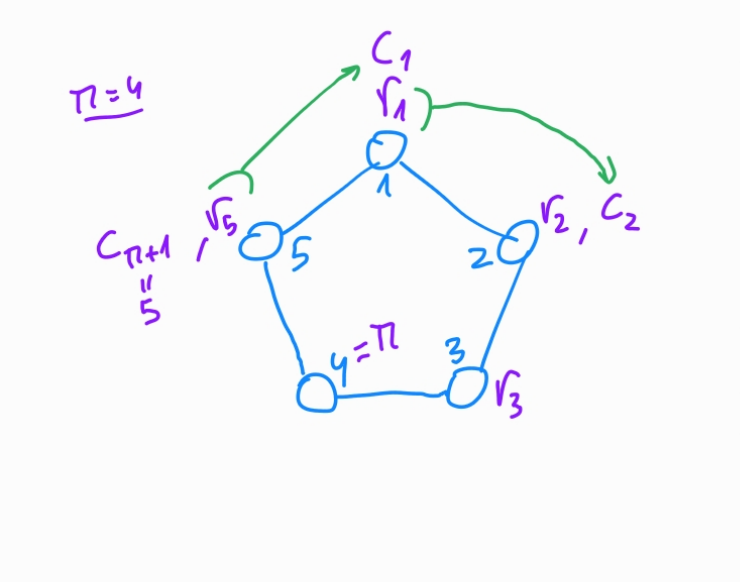
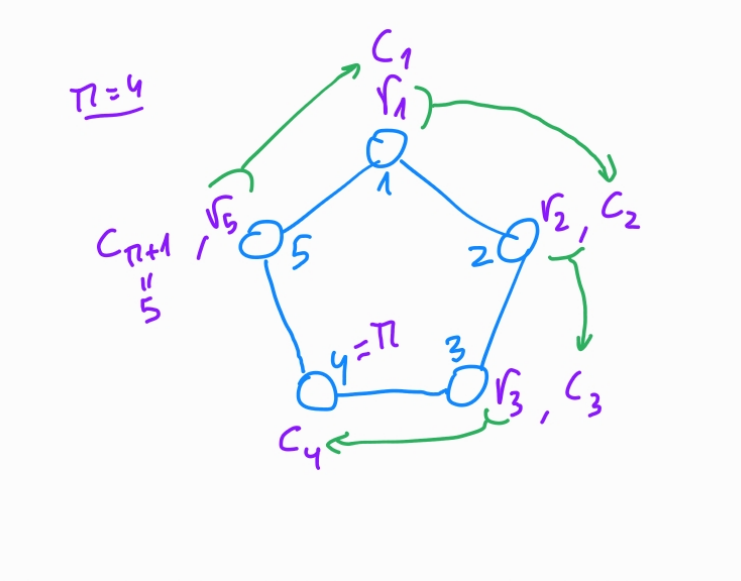
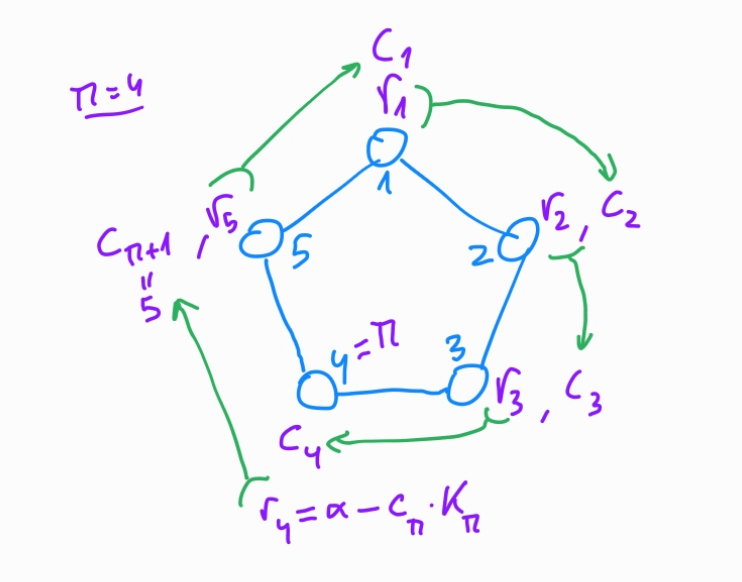
Generate $r_i \in^R \mathbb{Z_p}$
Compute $c_{i+1}$ from $r_i$
Link $r_{\pi}$ with $c_{\pi}$

You can scroll down the images through the step-by-step diagrams.

It reminds in some way to the approach to close a box like the one in the picture:

Verification

check $p \tilde{K} \stackrel{?}{=} 0$
- to ensure that $\tilde{K} \in G$ (and not in a cofactor group of $G$)
for $i = 1, 2, \ldots, n$, replacing $n+1 \rightarrow 1$ $$ c'_{i+1} = \mathcal{H}_n (m, [r_i G + c_i K_i], [r_i \mathcal{H}_p (K_i) + c_i \tilde{K}]) $$

check $c_1 \stackrel{?}{=} c'_i$

c[0] = c1
for j in range(0, len(R)):
    i = mod(j, len(R))
    i1 = mod(j+1, len(R))
    c[i1] = hash(R, m, r[i] * g + c[i] * R[i],
                 r[i] * hashToPoint(R[i]) + c[i] * key_image, p)


assert c1 == c[0]

bLSAG ring signatures overview

Setup

Signature

Step by step (simplified):

Verification

Links