Lagrange Polynomial Interpolation and Shamir secret sharing

2021-10-10

If you read this post, be aware that I’m not a mathematician, I’m just an amateur on math studying in my free time, and this article is just an attempt to try to sort the notes that I took while learning about Lagrange polynomial interpolation and Shamir’s secret sharing.

Imagine that you have a secret (for example a private key that can decrypt a file), and you want to backup that secret. You can split the secret and give each slice to a different person, so when you need to reconstruct the secret you just need to put together all the parts. But, what happens if one of the parts gets corrupted, or is lost? The secret would not be recoverable. A better solution can be done if we use Shamir Secret Sharing, which allows us to split the secret in \(k\) different parts, and set a minimum threshold \(n\), which defines the number of required parts to recover the secret, so just by putting together any \(n\) parts we will recover the original secret.

This has interesting applications, such as social recovery of keys or distributing a secret and ensuring that cooperation is needed in order to recover it. In the following lines we will overview the concepts behind this scheme.

Lagrange polynomial interpolation

Lagrange interpolation is also used in many schemes that work with polynomials, for example in KZG Commitments (an actual implementation can be found here).

The main idea behind is the following: for any \(n\) distinct points over \(\mathbb{R}^2\), there is a unique polynomial \(p(x) \in \mathbb{R[x]}\) of degree \(n-1\) which goes through all of them. From the ‘other side’ point of view, this means that if we have a polynomial of degree \(n-1\), we can take \(n\) points (or more) from it, and we will be able to recover the original polynomial from those \(n\) points.

We can see this starting with a line. If we are given any two points \(P_0=(x_0, y_0)\) and \(P_1=(x_1, y_1)\) from that line, we are able to recover the original line.

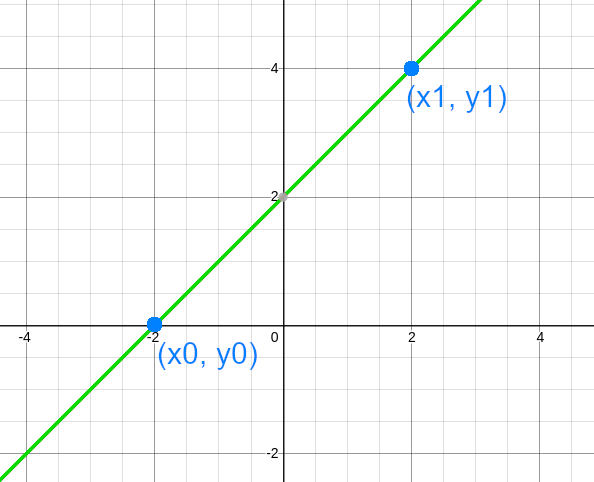
We can map this into the previous idea, seeing that our line is a degree \(1\) polynomial, so, if we pick \(2\) points from it, we later can recover the original line.

Same happens with polynomials of degree \(2\). Let \(p(x)\) be a polynomial of degree \(2\) defined by \(p(x)= x^2 - 5x - 6\). We can create infinity of polynomials of degree \(2\) that go through \(2\) points, but with 3 points there is a unique polynomial degree \(2\)

As the degree is \(2\), if we pick \(3\) points from the polynomial, we will be able to reconstruct it.

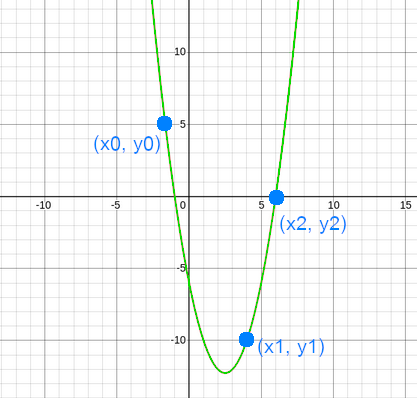
This is generalized by using Lagrange polynomial interpolation, which defines:

For a set of points \((x_0, y_0), (x_1, y_1), ..., (x_n, x_n)\),

\[ I(x) = \sum_{i=0}^n y_i l_i(x)\newline where \space\space\space l_i(x) = \prod\_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i - x_j} \]

Shamir’s secret sharing

As we’ve seen, for a degree \(n-1\) polynomial we can pick \(n\) or more points and we will be able to reconstruct the original polynomial from it. This is the main idea used in Shamir’s secret sharing.

Let \(s\) be our secret. We want to generate \(k\) pieces and set a threshold \(n\) which is the minimum number of pieces that are needed to reconstruct the secret \(s\). We can define a polynomial of degree \(n-1\), and pick \(k\) points from that polynomial, so in this way with just putting together \(n\) points of \(k\) we will be able to reconstruct the original polynomial. And, we can place our secret \(s\) in the constant term of the polynomial (the one that has \(x^0\)), in this way, when we reconstruct the polynomial using \(n\) out of \(k\) points, we will be able to recover the secret \(s\).

We can see this with an example with actual numbers (we will use small numbers): Imagine that we want to generate \(5\) pieces from our secret, and define that just by putting together \(3\) of the pieces we can recover the secret, this means setting \(n=3\) and \(k=5\). Then we will generate a polynomial of degree \(n-1=2\), by \(p(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2\), where \(\alpha_0 = s\) (the secret).

We will work over a finite field of size \(p\), where \(p\) is a prime number. For our example we will work over \(\mathbb{F}_{19}\), in real world we would work with much more bigger field. You can find an example without finite fields in Wikipedia.

Let our secret be \(s=14\). We now generate our polynomial of degree \(n-1=2\), where \(s\) will be the constant coefficient: \(p(x)= s + \alpha_1 x^1 + \alpha_2 x^2\). We can set \(\alpha_1\) and \(\alpha_2\) into any random value, as example \(\alpha_1=4\) and \(\alpha_2=6\). So we have our polynomial: \(p(x) = 14 + 4 x + 6 x^2\).

Now that we have the polynomial, we can pick \(k\) points from it, using incremental indexes for the \(x\) coordinate: \(P_1=(1, p(1)), P_2=(2, p(2)), \space\ldots\space, P_k=(k, p(k))\). With the numbers of our example this is (remember, we work over \(\mathbb{F}\_{19}\)):

\[ p(x) = 14 + 4 x + 6 x^2,\newline p(1)=14 + 4 \cdot 1 + 6 \cdot 1^2 = 24 \space (mod \space 19) = 5\newline p(2)=14 + 4 \cdot 2 + 6 \cdot 2^2 = 46 \space (mod \space 19) = 8\newline p(3)=14 + 4 \cdot 3 + 6 \cdot 3^2 = 80 \space (mod \space 19) = 4\newline p(4)=14 + 4 \cdot 4 + 6 \cdot 4^2 = 126 \space (mod \space 19) = 12\newline p(5)=14 + 4 \cdot 5 + 6 \cdot 5^2 = 184 \space (mod \space 19) = 13 \]

So our \(k\) points are: \((1,5), (2,8), (3,4), (4,12), (5,13)\). We can distribute these points as our ‘secret parts’. In order to recover the secret, we need at least \(n=3\) points, for example \(P_1\), \(P_3\), \(P_5\), and we compute the Lagrange polynomial interpolation to recover the original polynomial (remember, we work over \(\mathbb{F}\_{19}\)):

\[ I(x) = \sum_{i=0}^n y_i l_i(x) \space\space where \space\space\space l_i(x) = \prod\_{0 \leq j \leq n \\ j\neq i} \frac{x-x_j}{x_i - x_j} \]

\[ l_1(x) = \frac{x-3}{1-3} \cdot \frac{x-5}{1-5} = \frac{x-3}{17} \cdot \frac{x-5}{15}=\frac{x^2+11x+15}{8}\newline l_3(x) = \frac{x-1}{3-1} \cdot \frac{x-5}{3-5} = \frac{x-1}{2} \cdot \frac{x-5}{17} =\frac{x^2+13x+5}{15}\newline l_5(x) = \frac{x-1}{5-1} \cdot \frac{x-3}{5-3} = \frac{x-1}{4} \cdot \frac{x-3}{2} = \frac{x^2 + 15x + 3}{8}\newline \]

\[ I(x) = y_2 \cdot l_2(x) + y_4 \cdot l_4(x) + y_5 \cdot l_5(x)\newline = 5 \cdot (\frac{x^2+11x+15}{8}) + 4 \cdot (\frac{x^2+13x+5}{15}) + 13 \cdot (\frac{x^2 +15x + 3}{8})\newline = \frac{5x^2+17x+18}{8} + \frac{4x^2+14x+1}{15} + \frac{13x^2+5x+1}{8}\newline = 3x^2+14x+7 + 18x^2+6x+14 + 4x^2+3x+12\newline = 6x^2 + 4x + 14 \]

We can now take the constant coefficient, or just evaluate the obtained polynomial at 0, \(p(0) = 6 \cdot 0^2 + 4 \cdot 0 + 14 = 14\), and we obtain our original secret \(s=14\).

Conclusions

As an example of an use case of Shamir Secret Sharing we can think of social recovery of keys, there is an useful implementation of this scheme is used in the banana split by Parity. Also, here it is an implementation of the scheme in Go&Rust done a couple of years ago: https://github.com/arnaucube/shamirsecretsharing.

Lagrange Interpolation in its own way, is a very useful tool in many schemes, it is also used in KZG Commitments, in zkSNARKs, zkSTARKs, PLONK, etc. In most of the schemes where polynomials are involved it becomes a very useful tool.